一、图的基本概念
(一)、图的定义和术语
1.图的定义:
一个图(G)定义为一个偶对(V,E) ,记为G=(V,E) 。图由顶点和边组成
其中:
V是顶点(Vertex)的非空有限集合,记为V(G);图G中所有顶点的集合
E是无序集V&V的一个子集,记为E(G) 图G中所有边的集合
“V&V”表示顶点集合V与自身的笛卡尔积
其元素是图的弧(Arc)。
2.空图:将顶点集合为空的图称为空图。
3.形式化定义:

4. 弧(Arc) :
表示两个顶点v和w之间存在一个关系,用顶点偶对<v,w>表示。通常根据图的顶点偶对将图分为有向图和无向图。
5.有向图(Digraph):
(1)若图G的关系集合E(G)中,顶点偶对<v,w>的v和w之间是有序的,称图G是有向图。
(2)在有向图中,若
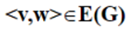
,表示从顶点v到顶点w有一条弧。 其中:
v称为弧尾(tail)或始点(initial node),
w称为弧头(head)或终点(terminal node) 。
6.无向图(Undigraph):
(1)若图G的关系集合E(G)中,顶点偶对<v,w>的v和w之间是无序的,称图G是无向图。
(2)在无向图中,若
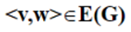
,有

,即E(G)是对称,则用无序对(v,w) 表示v和w之间的一条边(Edge),因此(v,w)和(w,v)代表的是同一条边。
7.完全无向图:
(1)定义1:对于无向图,若图中顶点数为n ,用e表示边的数目,则
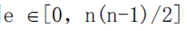
。具有n(n-1)/2条边的无向图称为完全无向图。
(2)定义2:对于无向图G=(V,E),若

,当vi≠vj时,有
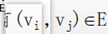
,即图中任意两个不同的顶点间都有一条无向边,这样的无向图称为完全无向图。
8.完全有向图:
(1)定义1:对于有向图,若图中顶点数为n ,用e表示弧的数目,则
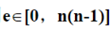
。
具有n(n-1)条边的有向图称为完全有向图。
(2)定义2:对于有向图G=(V,E),若
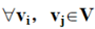
,当vi ≠vj时,有
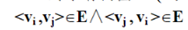
,即图中任意两个不同的顶点间都有一条弧,这样的有向图称为完全有向图。
9.稀疏图与稠密图:
有很少边或弧的图(e<n㏒n)的图称为稀疏图,反之称为稠密图。
10.权(Weight):
与图的边和弧相关的数。权可以表示从一个顶点到另一个顶点的距离或耗费。
11.子图和生成子图:
设有图G=(V,E)和G’=(V’,E’)
(1)若
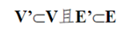
,则称图G’是G的子图;
(2)若
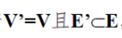
,则称图G’是G的一个生成子图。
12.顶点的连接与关联
(1)顶点的邻接(Adjacent):
对于无向图G=(V,E),若
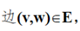
则称顶点v和w 互为邻接点,即v和w相邻接。边(v,w)依附(incident)于顶点v和w。
(2)顶点的关联:
对于有向图G=(V ,E),若有向
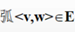
,则称顶点v “邻接到”顶点w,顶点w “邻接自”顶点v ,弧<v,w> 与顶点v和w “相关联”
13.顶点的度、入度、出度:
(1)对于无向图G=(V,E),

,图G中依附于vi的边的数目称为顶点vi的度(degree),记为TD(vi)
在无向图中,所有顶点度的和是图中边的2倍。 即∑TD(vi)=2e i=1, 2, …, n ,e为图的边数。
(2)对于有向图G=(V,E),若

,
图G中以vi作为起点的有向边(弧)的数目称为顶点vi的出度(Outdegree),记为OD(vi) ;
以vi作为终点的有向边(弧)的数目称为顶点vi的入度(Indegree),记为ID(vi) 。
顶点vi的出度与入度之和称为vi的度,记为TD(vi) 。即TD(vi)=OD(vi)+ID(vi)。
14.路径(Path)、路径长度、回路(Cycle) :
(1)对无向图G=(V,E),若从顶点vi经过若干条边能到达vj,称顶点vi和vj是连通的,又称顶点vi到vj有路径。
(2)对有向图G=(V,E),从顶点vi到vj有有向路径,指的是从顶点vi经过若干条有向边(弧)能到达vj。路径是图G中连接两顶点之间所经过的顶点序列。即Path=vi0vi1…vim ,vij
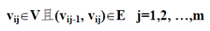
(3)路径上边或有向边(弧)的数目称为该路径的长度。
(4)在一条路径中,若没有重复相同的顶点,该路径称为简单路径;
(5)第一个顶点和最后一个顶点相同的路径称为回路(环);
(6)在一个回路中,若除第一个与最后一个顶点外,其余顶点不重复出现的回路称为简单回路(简单环)。
15. 连通图、图的连通分量:
(1)对无向图G=(V,E),若
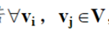
,vi和vj都是连通的,则称图G是连通图
否则称为非连通图。
(2)若G是非连通图,则极大的连通子图称为G的连通分量。
(3)对有向图G=(V,E),若

,
都有以vi为起点, vj 为终点以及以vj为起点,vi为终点的有向路径,称图G是强连通图,否则称为非强连通图。
(4)若G是非强连通图,则极大的强连通子图称为G的强连通分量
“极大”的含义:指的是对子图再增加图G中的其它顶点,子图就不再连通
16.生成树、生成森林:
(1)一个连通图(无向图)的生成树是一个极小连通子图,它含有图中全部n个顶点和只有足以构成一棵树的n-1条边,称为图的生成树。
(2)关于无向图的生成树的几个结论:
a.一棵有n个顶点的生成树有且仅有n-1条边;
b.如果一个图有n个顶点和小于n-1条边,则是非连通图
c.如果多于n-1条边,则一定有环;
d.有n-1条边的图不一定是生成树
(3)有向图的生成森林是这样一个子图,由若干棵有向树组成,含有图中全部顶点。
(4)有向树是只有一个顶点的入度为0 ,其余顶点的入度均为1的有向图。
17网:
每个边(或弧)都附加一个权值的图,称为带权图。带权的连通图(包括弱连通的有向图)称为网或网络。网络是工程上常用的一个概念,用来表示一个工程或某种流程。
(二)、图的抽象数据类型定义

二、图的存储结构
图的常用的存储结构有:邻接矩阵、邻接链表、十字链表、邻接多重表和边表。
(一)、邻接矩阵(数组)表示法
1.基本思想:
对于有n个顶点的图,用一维数组vexs[n]存储顶点信息,用二维数组A[n][n]存储顶点之间关系的信息。该二维数组称为邻接矩阵。在邻接矩阵中,以顶点在vexs数组中的下标代表顶点,邻接矩阵中的元素A[i][j]存放的是顶点i到顶点j之间关系的信息。
2.无向图的数组表示
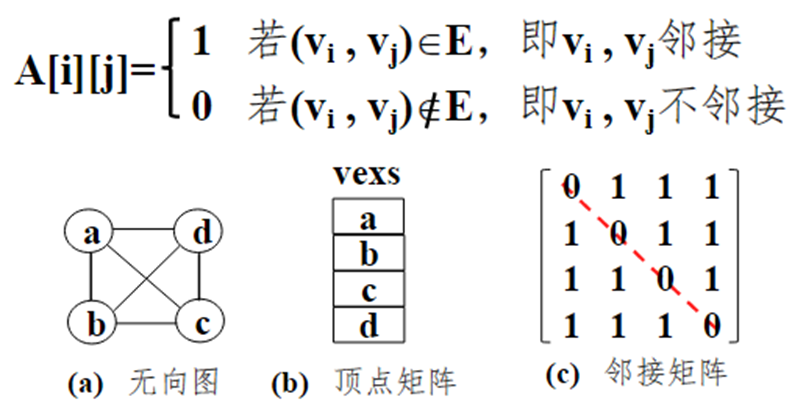
(1) 无权图的邻接矩阵
无向无权图G=(V,E)有n(n≧1)个顶点,其邻接矩阵是n阶对称方阵,如图所示。
(2) 带权图的邻接矩阵
无向带权图G=(V,E) 的邻接矩阵如图所示。

(3)无向图邻接矩阵的特性
a.邻接矩阵是对称方阵;
b.对于顶点vi,其度数是第i行的非0元素的个数;
c.无向图的边数是上(或下)三角形矩阵中非0元素个数。
3.有向图的数组表示
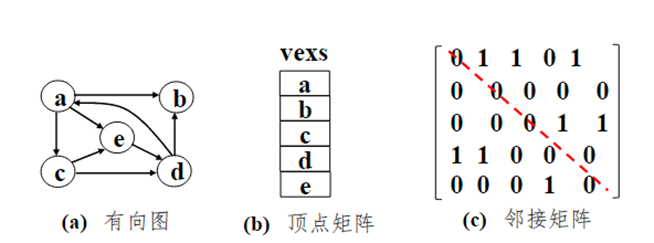
(1) 无权图的邻接矩阵
若有向无权图G=(V,E)有n(n≧1)个顶点,则其邻接矩阵是n阶方阵,如图所示。
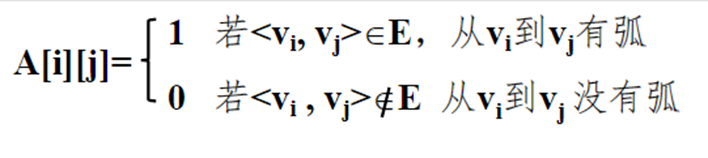
(2)带权图的邻接矩阵
有向带权图G=(V,E)的邻接矩阵如图所示。
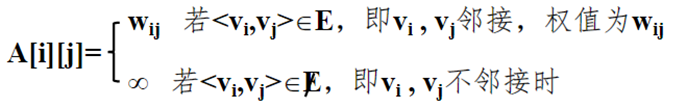
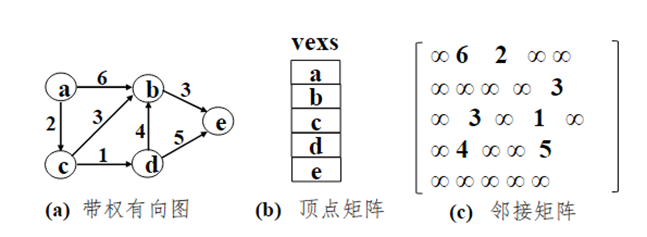
(3)有向图邻接矩阵的特性
a.对于顶点vi,第i行的非0元素的个数是其出度OD(vi);
b.第i列的非0元素的个数是其入度ID(vi) 。
c.邻接矩阵中非0元素的个数就是图的弧的数目。
3.图的邻接矩阵的操作
(1)图的邻接矩阵的实现,定义两个数组分别存储顶点信息(数据元素)和边或弧的信息(数据元素之间的关系) 。
其存储结构形式定义如下:
#define INFINITY MAX_VAL /* 最大值∞ */
/* 根据图的权值类型,分别定义为最大整数或实数 */
#define MAX_VEX 30 /* 最大顶点数目 */
typedef enum {DG, AG, WDG,WAG} GraphKind ;
/* {有向图,无向图,带权有向图,带权无向图} */
typedef struct ArcType
{
VexType vex1, vex2 ; /* 弧或边所依附的两个顶点 */
ArcValType ArcVal ; /* 弧或边的权值 */
ArcInfoType ArcInfo ; /* 弧或边的其它信息 */
}ArcType ; /* 弧或边的结构定义 */
typedef struct
{
GraphKind kind ; /* 图的种类标志 */
int vexnum , arcnum ; /* 图的当前顶点数和弧数 */
VexType vexs[MAX_VEX] ; /* 顶点向量 */
AdjType adj[MAX_VEX][MAX_VEX];
}MGraph ; /* 图的结构定义 */(2) 图的创建
AdjGraph *Create_Graph(MGraph * G)
{
printf(“请输入图的种类标志:”) ;
scanf(“%d”, &G->kind) ;
G->vexnum=0 ; /* 初始化顶点个数 */
return(G) ;
}(3) 图的顶点定位
图的顶点定位操作实际上是确定一个顶点在vexs数组中的位置(下标) ,其过程完全等同于在顺序存储的线性表中查找一个数据元素。
算法实现:
int LocateVex(MGraph *G , VexType *vp)
{
int k ;
for (k=0 ; k<G->vexnum ; k++)
if (G->vexs[k]==*vp) return(k) ;
return(-1) ; /* 图中无此顶点 */
}(4) 向图中增加顶点
向图中增加一个顶点的操作,类似在顺序存储的线性表的末尾增加一个数据元素。
算法实现:
int AddVertex(MGraph *G , VexType *vp)
{
int k , j ;
if (G->vexnum>=MAX_VEX)
{
printf(“Vertex Overflow !\n”) ; return(-1) ;
}
if (LocateVex(G , vp)!=-1)
{
printf(“Vertex has existed !\n”) ; return(-1) ;
}
k=G->vexnum ; G->vexs[G->vexnum++]=*vp ;
if (G->kind==DG||G->kind==AG)
for (j=0 ; j<G->vexnum ; j++)
G->adj[j][k].ArcVal=G->adj[k][j].ArcVal=0 ;
/* 是不带权的有向图或无向图 */
else
for (j=0 ; j<G->vexnum ; j++)
{
G->adj[j][k].ArcVal=INFINITY ;
G->adj[k][j].ArcVal=INFINITY ;
/* 是带权的有向图或无向图 */
}
return(k) ;
}(5) 向图中增加一条弧
根据给定的弧或边所依附的顶点,修改邻接矩阵中所对应的数组元素。
算法实现:
int AddArc(MGraph *G , ArcType *arc)
{
int k , j ;
k=LocateVex(G , &arc->vex1) ;
j=LocateVex(G , &arc->vex2) ;
if (k==-1||j==-1)
{
printf(“Arc’s Vertex do not existed !\n”) ;
return(-1) ;
}


Comments NOTHING